This is a paper I published Educational Theory back in 2011 about the factors shaping the rise of quantification in education research.  It still seems relevant to a lot of issues in the field educational policy. 

Here’s an overview of the argument:

In this paper I explore the historical and sociological elements that have made educational researchers dependent on statistics – as a mechanism to shore up their credibility, enhance their scholarly standing, and increase their influence in the realm of educational policy.  I begin by tracing the roots of the urge to quantify within the mentality of measurement that arose in medieval Europe, and then explore the factors that have pressured disciplines and professions over the years to incorporate the language of mathematics into their discourse.  In particular, this pattern has been prominent for domains of knowledge and professional endeavor whose prestige is modest, whose credibility is questionable, whose professional boundaries are weak, and whose knowledge orientation is applied.  I show that educational research as a domain – with its focus on a radically soft and thoroughly applied form of knowledge and with its low academic standing – fits these criteria to a tee.   Then I examine two kinds of problems that derive from educational researchers’ seduction by the quantitative turn.  One is that this approach to educational questions deflects attention away from many of the most important issues in the field, which are not easily reduced to standardized quanta.  Another is that by adopting this rationalized, quantified, abstracted, statist, and reductionist vision of education, education policymakers risk imposing reforms that will destroy the local practical knowledge that makes the ecology of the individual classroom function effectively.  Quantification, I suggest, may be useful for the professional interests of educational researchers but it can be devastating in its consequences for school and society.

The Lure of Statistics for Educational Researchers
Published 2011 in Educational Theory, 61:6

Philosophy is written in this grand book, the universe, which stands continually open to our gaze, but the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed.  It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.[1]

                                                                        –Galileo

During the course of the twentieth century, educational research yielded to the lure of Galileo’s vision of a universe that could be measured in numbers.[2]  This was especially true in the United States, where quantification had long enjoyed a prominent place in public policy and professional discourse.  But the process of reframing reality in countable terms began eight centuries earlier in Western Europe, where it transformed everything from navigation to painting, then arrived fully formed on the shores of the New World, where it shaped the late-blooming field of scholarship in education.  Like converts everywhere, the new American quantifiers in education became more Catholic than the pope, quickly developing a zeal for measurement that outdid the astronomers and mathematicians that preceded them.  The consequences for both education and educational research have been deep and devastating.

In this paper I explore the historical and sociological elements that have made educational researchers dependent on statistics – as a mechanism to shore up their credibility, enhance their scholarly standing, and increase their influence in the realm of educational policy.  I begin by tracing the roots of the urge to quantify within the mentality of measurement that arose in medieval Europe, and then explore the factors that have pressured disciplines and professions over the years to incorporate the language of mathematics into their discourse.  In particular, this pattern has been prominent for domains of knowledge and professional endeavor whose prestige is modest, whose credibility is questionable, whose professional boundaries are weak, and whose knowledge orientation is applied.  I show that educational research as a domain – with its focus on a radically soft and thoroughly applied form of knowledge and with its low academic standing – fits these criteria to a tee.   Then I examine two kinds of problems that derive from educational researchers’ seduction by the quantitative turn.  One is that this approach to educational questions deflects attention away from many of the most important issues in the field, which are not easily reduced to standardized quanta.  Another is that by adopting this rationalized, quantified, abstracted, statist, and reductionist vision of education, education policymakers risk imposing reforms that will destroy the local practical knowledge that makes the ecology of the individual classroom function effectively.  Quantification, I suggest, may be useful for the professional interests of educational researchers but it can be devastating in its consequences for school and society.

The Roots of Quantification in Educational Research

Alfred Crosby locates the roots of quantification in Western Europe in the thirteenth century.[3]  What it gradually displaced was a worldview without standardized modes of measurement, which he labels the “venerable model.”  From the perspective of this model, the world was heterogeneous, where differences were qualitative rather than quantitative and thus reality could not be reduced to common units of measurement.  Fire rose and rocks fell because that was their nature, with fire returning to the sphere of fire and rocks to the sphere of earth in a four-sphere universe where air and water separated them from each other.  Measuring the distance between spheres was as nonsensical as measuring the distance between God and man.  Time and space also had a qualitative character.  Numbers were difficult to work with, since they were recorded using the first letter of the Latin word for each quantity, which meant that quantities were words and formulas were sentences.

Crosby says that quantification arose in Europe because of efforts by ordinary men to solve practical problems.  Factors like growing trade, increased travel, and an emerging cash economy urged the process forward.  As time started to become money, merchants called for reliable measures of distance, time, and accounts, which pushed sailors to develop new measures of navigation, mechanics to develop clocks, and merchants to develop double-entry bookkeeping.  They needed to keep accurate accounts, and they needed figures that could be easily manipulated, so Arabic numbers gradually made headway.  But at the heart of this process, according to Crosby, was a fundamental shift in mentality toward thinking of the world in quanta.  The quick spread of factors like cash transactions and church-tower clocks began to educate the populace in a new quantitative world in which things could be measured in fixed units.

Theodore Porter picks up the story in the 19^th century, exploring how professions became quantifiers.[4]  The move toward quantification, he shows, was not the preferred option for most professionals.  Left to their own devices, professional groups over the years have generally chosen to establish their authority through consensus within the professional community itself.  But this approach only works if outsiders are willing to cede a particular area of expertise to the profession and rely on the soundness of its judgment.  He argues that what drove the professions to adopt quantification was a growing set of challenges to their professional authority.  Quantification allows a professional community to make arguments that carry weight and establish validity beyond a particular time, place, and community of authorship.[5]

Democracies in particular are suspicious of claims of elite authority, unwilling to bow to such claims as a matter of professional judgment without an apparently objective body of evidence that establishes their independent credibility.  The United States embraced numbers early in its history, for political and moral reasons as well as concerns about elite authority.  The decennial census was a central mechanism for establishing the legitimacy of representative government, and in the early 19^th century counting became a means for assessing the state of public morality.  By the 1830s, the U.S. experienced an explosion of the quantification of public data, with the proliferation of statistics societies and quantitative reports.[6]

For our understanding of the eventual conversion of educational research to the credo of measurement, however, Porter’s most salient insight is that the adoption of quantification by a profession is a function of its weakness.[7]  If a profession has sufficiently strong internal coherence and high social status, it will assert its right to make pronouncements within its domain of expertise on its own authority.  To resort to supporting one’s claims with numbers is to cede final authority to others.  Only those professions that are lacking in inner strength and outer esteem must stoop to quantify.  In particular, Porter notes that the professions and academic disciplines that are most prone to deploying numbers in support of their claims are those whose domain of knowledge is the most applied.  Compared with a domain of pure knowledge, where the boundaries between its zone of expertise and the practical world are sharply defined, applied fields find themselves operating in a terrain that is thoroughly mingled with practical pursuits and thus difficult to defend as an exclusive territory.[8]  Here professionals find themselves subject to the greatest external pressures and the strongest need to demonstrate the credibility of the claims through quantitative means.  Such is the terrain of educational research.

American educational researchers in the early 20^th century took the plunge into quantification.  This was the era of Edward L. Thorndike and Lewis Terman; of the proliferation of intelligence tests and other standardized assessments in schools; and of the development of scientific curriculum, which built on testing to track students into suitable studies.  It was the period chronicled by Stephen Jay Gould in The Mismeasure of Man and by Nicholas Lemann in The Big Test.[9]  I argue that  educational research took the quantitative turn so early and so deeply of its position as a domain of knowledge that is both very soft and very applied.  As a result of this situation, educational researchers have been hard pressed to accumulate knowledge, defend it from outsiders, develop a coherent account of the field, build on previous work, and convince policymakers to take their findings seriously.  Quantification brought the hope of shoring up professional authority.[10]

The difference between hard and soft fields of study is familiarly understood in terms of distinctions like quantitative and qualitative, objective and subjective, and definitive and interpretive approaches.  Of course, the hard-soft distinction is difficult to establish philosophically, but one thing we do know for sure is that the so-called hard sciences have an easier job of establishing their claims of validity than their soft knowledge colleagues.  In this polarity, the knowledge that educational researchers develop is perhaps the softest of the soft fields, which prevents them from being able to make strong claims about their findings much less to accumulate those claims.  Like other social science domains, they have to deal with willful actors operating within extraordinarily complex social settings.  But in addition, educational researchers are stuck trying to understand matters like teaching and learning within an organizational structure that is both loosely coupled and deeply nested, which makes it very hard to generalize across contexts.

The difference between pure and applied fields of study is generally understood in terms of distinctions like theoretical and practical, intellectually oriented and application oriented.  Of course, every pure discipline has claims to usefulness and every applied field has aspirations to theory.  But the key difference in practice is that pure disciplines are more in control of their intellectual work and less dependent on context, whereas  applied fields are stuck with the task of pursuing whatever their knowledge domain demands.  For educational researchers this means tackling the problems that arise from the professional problems of schooling the populace.  Instead of exploring issues for which their theories might be effective, they have to plunge into problems for which their theories and methods are inadequate.  Unlike researchers in pure domains, educational scholars have to do what is needed rather than what they are good at.

The relentlessly soft and applied character of the knowledge domain that educational researchers occupy helps explain the lowly status of the field within the university; and it also helps us understand why scholars in other academic fields, educational practitioners, and educational policymakers all feel free to offer their own opinions about education without bowing to the authority of its anointed experts.  This situation also helps us understand why educational researchers have been so eager to embrace the authority of statistics in their effort to be heard and taken seriously in the realms of university, practice, and policy.  If numbers are the resort of the weaker professions, as Porter argues, then educational research has the very strongest of incentives to adopt quantitative methods.  So the field has done what it can to cloak itself in the organizational and methodological robes of the hard-pure disciplines.

Educational researchers have come to the altar of quantification out of weakness, in the hope that their declarations of faith in the power of numbers will grant them newfound respect, gain them the trust of practitioners and policymakers, and enable them to exert due influence in the educational domain.  But this 20^th century conversion has not come without cost.  I focus on two major problems that have emerged from the shift to numbers in education.

One Problem with Quantifying Educational Research:
Missing the Point

The first problem with the quantitative turn in educational research is that it provides researchers with a strong incentive to focus on what they can measure statistically rather than on what is important.  It is a case of what Abraham Kaplan called the Drunkard’s Search, in which a drunk is looking for lost car keys – not in the dark where he lost them but under the streetlight where he can see better.[11]  It allows researchers to be methodologically sophisticated at exploring educational issues that do not matter.  Theodore Porter argues that this problem has been particularly pronounced in the United States, where the public policy process unduly demands, and is distorted by, quantitative “methods claiming objectivity,” which “often measure the wrong thing.”  He goes on to explain:

As an abstract proposition, rigorous standards promote public responsibility and may very well contribute to accountability, even to democracy.  But if the real goals of public action must be set aside so that officials can be judged against standards that miss the point, something important has been lost.  The drive to eliminate trust and judgment from the public domain will never completely succeed.  Possibly it is worse than futile.[12]

As an educational researcher, I have had my own experience with the problem of measuring the wrong thing.  This case can serve as a cautionary tale.  My first book, which emerged from my doctoral dissertation, was grounded in data with a strong quantitative component.  The numbers I constructed in the data-gathering and analysis phase of the study enabled me to answer one question rather definitively.  But it took a very long time to develop these quanta, which was particularly galling since it turned out that the most interesting questions in the study were elsewhere, emerging from the qualitative data.

The book, The Making of an American High School, was a study of the first public high school in Philadelphia, from its opening in 1838 to its reconfiguration in 1939.[13]  Funded as part of a large grant from the National Institute of Education (NIE) to my advisor, Michael Katz, this study called in part for coding data from a sample students attending the school over an 80-year period and then linking these students to their family’s records in the federal census manuscripts, where individuals could be found by name and address.  A key reason that NIE was willing to fund this project in 1979 (at $500,000, it was the largest historical grant they had ever made) was the prime place in the grant proposal given to a rigorous quantitative analysis of the relationship between school and work in the city during this period.  For the study I selected a sample of Central High School students in every federal census year from 1840 to 1920, a total of 1,948 students.  I supervised a crew of 10 research assistants in the tedious task of coding data from school records for these students and then the enormously complex task of locating these students in census manuscripts and city directories for that year and coding that information as well.  In the next step, I punched all of the information on IBM cards (those were the days), worked with the data using several statistical packages (especially SPSS and SAS), created a variety of variables, tested them, and finally was able start data analysis.  I spent a total of four years working on my dissertation, from initial data gathering to the final manuscript, and fully half of that time I devoted to coding and analyzing my quantitative student data.

These quantitative data proved most useful for examining one issue about high school education in the period, the factors that shaped student attainment.  What kind of influence did factors like social class, country of origin, birth order, prior school, and academic grades have on the ability of Central High school students to persist at the school and even graduate?  To analyze this issue, I used multiple classification analysis,  a form of multiple regression using dummy variables that allows the research to consider the impact of non-interval data such as social class as well as interval data such as grade point average.  The dependent variable in the key equations was the chance of graduation (1 = yes, 0 = no) and the independent variables were major factors that might help explain this outcome.  The primary finding was that social class had no significant impact on graduation; the graduation rates were comparable for students across the class scale.  The only factor that significantly influenced graduation, in fact, was student grades.

This was not an uninteresting finding.  It was certainly counterintuitive that class would not be a factor in 19^th century educational success, since it proved to be a very important factor in 20^th century schooling.  And I could not have found this out without turning my data into quanta and analyzing them statistically.  So in my dissertation I proudly displayed these quantitative data spread across no fewer than 49 tables.[14]  As I worked for the next several years to write a book based on the dissertation, I sought to include as much of the number crunching information as I could.  This was in line with an old Hollywood adage:  If you spent a lot of money on a film, you need to show it on the screen.  As a result, I crammed as many tables as I could in the book manuscript and then asked my colleague, David Cohen, to read it for me.  His comments were generous and helpful to me in framing the book, but it was his opening line that knocked me back.  “All of these tables and the analysis that goes with them,” he said, “seem to add up to a very long footnote in support of the statement:  Central High School had meritocratic attainment.”

So I had spent two years of my life on a footnote.  That would not have been such a bad thing if the point being footnoted was the central point of the book.  But it was not.  It turned out that the most interesting issues that emerged from the book were elsewhere, having nothing to do with the quantitative data I had so laboriously constructed and so dutifully analyzed.  The core insight that emerged from the Central case was not about meritocracy but about the way the American high school in the late 19^th and early 20^th centuries emerged as both object and subject in the larger struggle between the liberal and the democratic for primacy in the American liberal democracy.  Established in order to express republican values and promote civic virtue, the high school quickly developed a second role as a mechanism for establishing social advantage for educational consumers seeking an edge in the competition for position.  At the same time that the common school system was established in the 1830s, allowing everyone in the community to gain public education under the same roof, the high school was established as a way provide distinction for a fortunate few.  And when the common schools filled up in the late 19^th century and demand for access to high school became politically irresistible, the school system opened up high school enrollment but at the same time introduced curriculum tracking.  This meant that access for the many did not dilute advantages for the few, who ended up in the upper track of the high school where they were on a trajectory for the exclusive realm of the university.  So the real Central High School story is about the way schools managed both to allow open access and to preserve exclusive advantage in the same institution.  In this way schools were not just responding to social pressures but also acting to shape a new liberal democratic society.

The point of this story for the purposes of the paper is that statistical work can lure educational researchers away from the issues that matter.  In many ways, statistical analysis is compellingly attractive to us as researchers in education.  It is a magnet for grant money, since policymakers are eager for the kind of apparently objective data that they think they can trust, especially when these data are coming from a low-status and professionally suspect field such as education.  It therefore increases our ability to be players in the game of educational policy, which is critically important in a professional field like ours.  At the same time it enhances our standing at our home institutions and in the broader educational research community, by providing us with the research assistants, doctoral advisees, travel budgets, and prospects for publication that serve as markers of academic status.  It provides us with a set of arcane skills in cutting edge methodologies, which are a major point of professional pride.  And once we have invested a lot of time and energy in developing these skills, we want to put them to good use in future projects.  The path of least resistance is to continue in the quantitative vein, looking around for new issues you can address with these methods.  When you are holding a hammer, everything looks like a nail.

Another Problem with Quantifying Educational Research:
Forcing a Rectangular Grid onto a Spherical World

So quantification is an almost irresistible fact of life in modern professional and disciplinary work.  This is especially true in a democracy, and even more so in a democracy like the U.S., where both professional and governmental authority are suspect.  The bias toward the quantitative is strongest in a professional domain that is low in status and applied in orientation – most particularly in the discounted field of education, afflicted with low status and a radically soft-applied arena of knowledge.  So educational policymakers have a preference for data that seem authoritative and scientific and that present a certain face validity.  Statistics are best suited to meet these needs, allowing policymakers to preface their proposals with the assertion that “research says” one policy would be more effective than another.  Since policymakers want these kinds of data, educational researchers feel compelled to supply them.

This is understandable, but the consequences for educational policy are potentially devastating.  One problem with this, as we saw in the last section, is that quantification may deflect researcher attention away from educational issues that are more important and salient.  Another problem, however, is that quantifying research on education can radically reduce the complexity of the educational domain that is visible to policymakers and then lead them to construct policies that fit the normalized digital map of education rather than the idiosyncratic analog terrain of education.  Under these circumstances, statistical work in education can lead to policies that destroy the ecology of the classroom in the effort to reform it.

In his book Seeing Like a State, James Scott explores the problems that arise when states instigate social reforms based on a highly rationalized, abstracted, and reductionist knowledge of society.[15]  His analysis provides a rich way to understand the kind of damage that educational policy, informed primarily by quantitative data, can do to the practice of schooling.  The connection between statistics and the state is both etymological and substantive.  The Oxford English Dictionary identifies the roots of the word “statistic” in the term “statist,” with the earliest meanings best rendered as “pertaining to statists or to statecraft.”[16]  Daniel Headrick shows that statistics first emerged in public view in the 17^th century under the label “political arithmetic,” arising in an effort to measure public health and the mercantilist economy.[17]  So over the years, seeing like a state has come to mean viewing society through statistics.

Following Scott, I argue that the statistical view of education takes the form of a grid, which crams the complexities of the educational enterprise into the confines of ledgers, frequency tables, and other summary quantitative representations that are epistemic projections from the center of the state to the periphery of educational practice.  Scott notes that part of the appeal of the grid for states is its esthetic: it looks neat, clean, and orderly, like modernist architecture.  In part the appeal is power: the ability to impose the unnatural grid on the world is an expression of the state’s ability to impose its own order.  In part the appeal is rationalization: the grid reflects a plan for how the world should be as the projection of a rational plan instead of as the result of chance, negotiation, or social compromise.  And in part the appeal is its utility: the grid allows for easy measurement, identification, and infinite subdivision. The key problem with this attraction to the grid is that policymakers tend to take these representations literally, which leads to reforms in which they seek to impose the rectangular grid of their vision onto the spherical world of education.

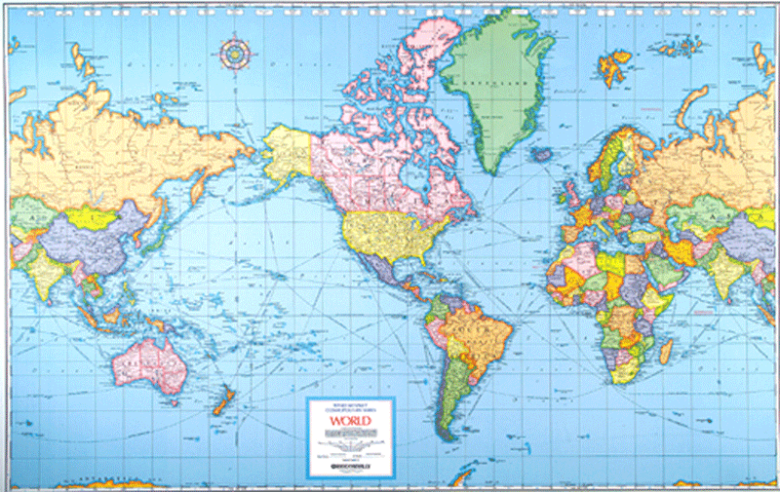
The image that comes to mind in thinking of both the utility and the danger of the grid is the Mercator projection in cartography, which is the example with which Crosby (1997, pp. 236-7) closes his book on The Measure of Reality.[18]  This map was developed to help solve a particular problem, which was to find a way so that sailors on the open sea could construct the shortest course between two points with a straight line using bearings of a compass.  Since such a course in reality would be an arc on the surface of the earth, this posed a real difficulty on a two dimensional map.  Mercator’s answer was to make lines of longitude, which converge toward the poles, instead run parallel to each other, thus increasingly exaggerating the east-west dimension as one approached the poles.  And in order to maintain the same proportions in the north-south direction, he extended the distance between lines of latitude proportionally at the same time.  The result is a map that allows navigators to plot an accurate course with a straight line, which was an enormous practical benefit.  But in the process it created a gross distortion of the world, which has convinced schoolchildren for centuries that Greenland is enormous and Africa is tiny.[19]

Like Mercator’s projection, quantitative data on education can be useful for narrow purposes, but only if we do not reify this representation.  However, the temptation to reify these measures is hard to resist.  So policymakers routinely use scores in standardized tests as valid measures of meaningful learning in school.  They use quantifiable characteristics of teachers (pay, years of graduate education, years of experience, certification in subject) as valid measures of the qualities that make them effective.  They use measures of socioeconomic status and parental education and gender and race to “control for” the effects of these complex qualities on teaching and learning.  When they put all of these quantitative measures together into a depiction of the process of schooling, they have constructed a mathematical map of this institution that multiplies the distorting effect of each reification by the number of such variables that appear in the equation.  The result is a distorted depiction of schooling that by comparison makes the Mercator projection look like a model of representation.  Recall that Mercator only distorted two variables, longitude and latitude, for a real practical benefit in navigational utility; and you can always look at a globe in order to correct for the representational distortion in his map.  But the maps of schooling that come from the quantitative measures of educational researchers incorporate a vast array of such distortions, which are multiplied together into summary measures that magnify these distortions.  And there is no educational globe to stand as a constant corrective.  The only counter to the mounds of quantitative data on schooling that sit on the desks of educational policymakers is a mound of interpretive case studies, which hardly balances the scales.  Such studies are easy to dismiss in the language of objective measurement, since they can be depicted as subjective, context bound, and ungeneralizable.  They can neither be externally validated nor internally replicated.  So why take them seriously?

In addition to the danger of reification that comes from the use of statistics for educational policy, there is the danger of giving primacy to technical knowledge and in the process discounting the value and validity of local practical knowledge.  Technical knowledge is universalistic, abstracted from particular contexts, and applicable anywhere.  It allows us to generalize the real world by abstracting from the gritty complexities of this world according to rationalized categories and quantifiable characteristics that are independent of setting.  Its language is mathematics.  As a result, technical knowledge is the natural way for the modern state to understand its domain.

In local settings, however, knowledge often takes a less rationalized and more informal character.  Understandings arise from the interaction among people, their work, and the contexts within which they live.  These understandings incorporate experience from the past, social arrangements that have developed from this experience, and a concern about applying these understandings to recurring problems and serious threats.  This kind of knowledge, says Scott, focuses on matters that are too complex to be learned from a book, like when to plant and harvest crops.  It arises when both uncertainty and complexity are high and when the urgency to do something is great even though all the evidence is not yet in.  It involves not rules but rules of thumb, which means it depends on judgment to decide which rule of thumb applies in a particular case.  It relies on redundancy, so there are multiple measures of where things stand, multiple ways to pursue a single end, and multiple mechanisms for ensuring the most critical outcomes, so that life will not depend on a single fallible approach.  It is a reliable form of knowledge for the residents of the local ecology because the residents have a stake in the knowledge (it is not “academic”), it captures the particular experience of the local context over time, and it is the shared knowledge of the community rather than the knowledge of particular experts.

Scott’s depiction of local practical knowledge arises in particular from anthropology and the knowledge of peasants tilling the soil in the ecology of a village, but it applies equally well to the work of teaching and learning in the ecology of the classroom.  The knowledge required to survive and thrive in that setting is enormously complex, uncertainty is high, rules of thumb (instead of technical laws) dominate, context is everything, and redundancy of measures and actions is essential in order to know what is going on and to avoid doing harm.  The craft of teaching in the modern classroom in this sense is similar to the craft of farming in a premodern village.  And one key commonality is the incompatibility between the local practical knowledge in this setting and the technical knowledge of the nation state.  When the state intervenes in either setting with a plan for social reform, based on a reified quantified vision of how things work, little good can result.

When the state takes the quantified depiction of schooling that educational researchers provide and uses it to devise a plan for school reform, the best we can hope for is that the reform effort will fail.  As the history of school reform makes clear, this is indeed most often the outcome.  One reform after another has bounced off the classroom door without having much effect in shaping what goes on inside, simply because the understanding of schooling that is embodied in the reform is so inaccurate that the reform effort cannot survive in the classroom ecology.  At worst, however, the reform actually succeeds in imposing change on the process of teaching and learning in classrooms.  Scott provides a series of horror stories about the results of such an imposition in noneducational contexts, from the devastating impact of the collectivization of agriculture in the Soviet Union to the parallel effect of imposing monoculture on German forests.  The problem in all these cases is that the effort to impose an abstract technical ideal ends up destroying a complex distinctive ecology that depends on local practical knowledge.  The current efforts by states across the globe to impose abstract technical standards on the educational village bear the signs of another ecological disaster.

[1]  Quoted in Alfred W. Crosby, The Measure of Reality: Quantification and Western Society, 1250-1600  (New York: Cambridge University Press, 1997), 240.

[2] An early version of this paper was presented at the conference on “The Ethics and Esthetics of Statistics” of the research group on Philosophy and History of the Discipline of Education: Faces and Spaces of Educational Research, Catholic University Leuven, Belgium, November, 2009.  A later version was published as a chapter in Paul Smeyers and Marc Depaepe (Eds.), Educational Research: The Ethics and Aesthetics of Statistics (Dordrecht: Springer, 2010).

[3]  Crosby, The Measure of Reality.

[4] Theodore M. Porter, The Rise of Statistical Thinking, 1820-1900 (Princeton: Princeton University Press, 1986); Theodore M. Porter, Trust in Numbers: The Pursuit of Objectivity in Science and Public Life (Princeton: Princeton University Press, 1995).

[5]  Porter, The Rise of Statistical Thinking, ix, 225.

[6]  Porter, Trust in Numbers, 195-7.  Daniel R. Headrick, When Information Came of Age: Technologies of Knowledge in the Age of Reason and Revolution, 1700-1850  (New York: Oxford University Press, 2000), 78,87.

[7]  Porter, Trust in Numbers, xi, 228.

[8]  Porter, Trust in Numbers, 229.

[9]  Stephen J. Gould, The Mismeasure of Man (New York: Norton, 1981); Nicholas Lemann, The Big Test: The Secret History of the American Meritocracy (New York: Farrar, Straus, and Giroux, 2000).

[10]  In this discussion, I draw on the work of Tony Becher (1989) and my own application of his analysis to education (Labaree, 1998; 2004, chapter 4).

[11] Abraham Kaplan, The Conduct of Inquiry: Methodology for Behavioral Science (San Francisco: Chandler, 1964).

[12]  Porter, Trust in Numbers, 216.

[13] David F. Labaree, The Making of an American High School: The Credentials Market and the Central High School of Philadelphia, 1838-1939 (New Haven: Yale University Press, 1988).

[14] David F. Labaree, “The People’s College: A Sociological Analysis of Philadelphia’s Central High School, 1838-1939” ( PhD diss., University of Pennsylvania. 1983).

[15] James C. Scott, Seeing Like a State: How Certain Schemes to Improve the Human Condition Have Failed (New Haven: Yale University Press, 1998).

[16] Oxford English Dictionary (London: Oxford University Press, 2002).

[17]  Headrick, When Information Came of Age, 60.

[18] Crosby, The Measure of Reality, 236-7.

[19] Mercator projection map, http://www.culturaldetective.com/worldmaps.html (accessed October, 2009).