Why Test Scores CAN'T Evaluate Teachers
I'm going to have more to say about Jonah Rockoff's testimony before the New Jersey State Board of Education last week. See here and here for previous posts; Bruce Baker also opines in a must-read post.
But right now, I want to use a specific part Dr. Rockoff's presentation to address a very serious problem with the entire notion of test-based teacher accountability. Keep in mind that Rockoff talks about Student Growth Percentiles (SGPs), but the problem extends to just about any use of Value-Added Modeling (VAM) in teacher evaluation based on test scores. Go to 1:07 in the clip:
The key element here that distinguishes Student Growth Percentiles from some of the other things that people have used in research is the use of percentiles. It's there in the title, so you'd expect it to have something to do with percentiles. What does that mean? It means that these measures are scale-free. They get away from psychometric scaling in a way that many researchers - not all, but many - say is important.
Now these researchers are not psychometricians, who aren't arguing against the scale. The psychometricians as who create our tests, they create a scale, and they use scientific formulae and theories and models to come up with a scale. It's like on the SAT, you can get between 200 and 800. And the idea there is that the difference in the learning or achievement between a 200 and a 300 is the same as between a 700 and an 800.
There is no proof that that is true. There is no proof that that is true. There can't be any proof that is true. But, if you believe their model, then you would agree that that's a good estimate to make. There are a lot of people who argue... they don't trust those scales. And they'd rather use percentiles because it gets them away from the scale.
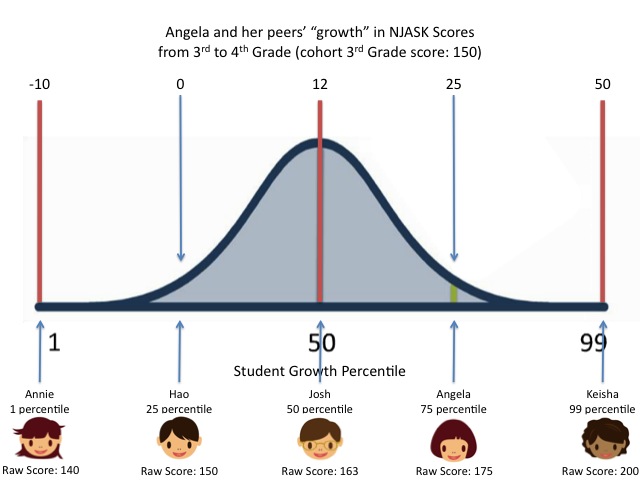
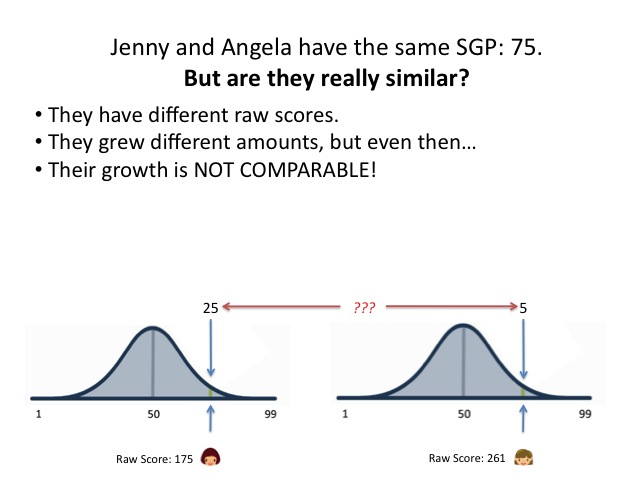
Let's state this another way so we're absolutely clear: there is, according to Jonah Rockoff, no proof that a gain on a state test like the NJASK from 150 to 160 represents the same amount of "growth" in learning as a gain from 250 to 260. If two students have the same numeric growth but start at different places, there is no proof that their "growth" is equivalent.
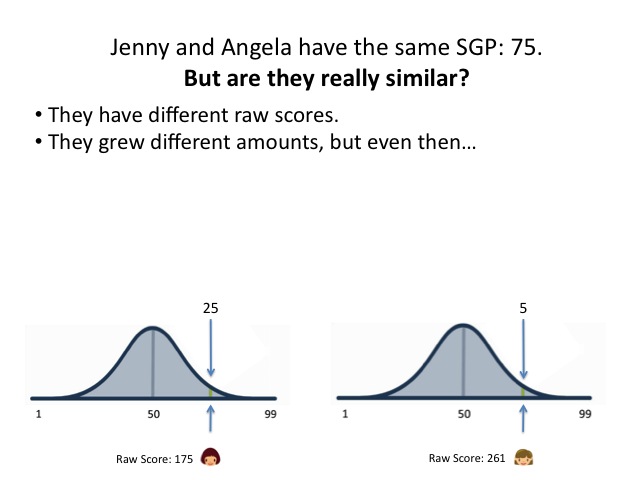
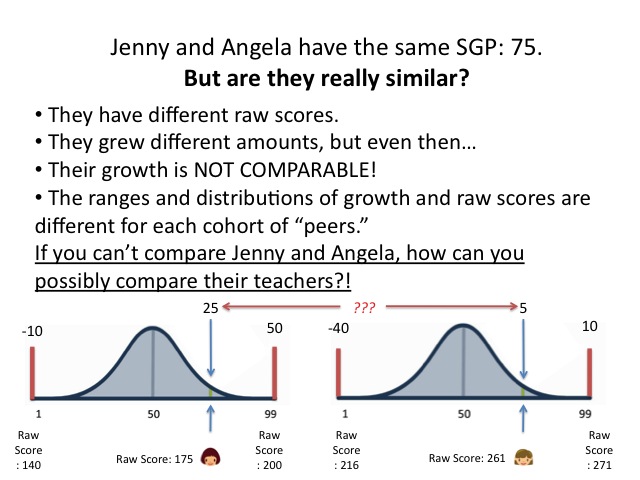
Now there's a corollary to this, and it's important: you also can't say that two students who have different numeric levels of "growth" are actually equivalent. I mean, if we don't know whether the same numerical gain at different points on the scale are really equivalent, how can we know whether one is actually "better" or "worse"? And if that's true, how can we possibly compare different numerical gains?
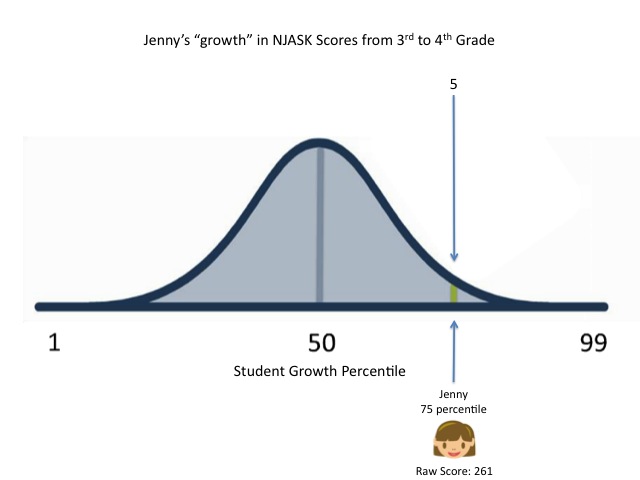
Keep this in mind as we, once again, go through a thought exercise with our friend, Jenny. You may remember from previous posts (here and here) that Jenny is a hypothetical 4th grader who just took the NJASK-4; we're looking to see the implications of Jenny's subsequent SGP. Here's how Jenny "grew" from last year:
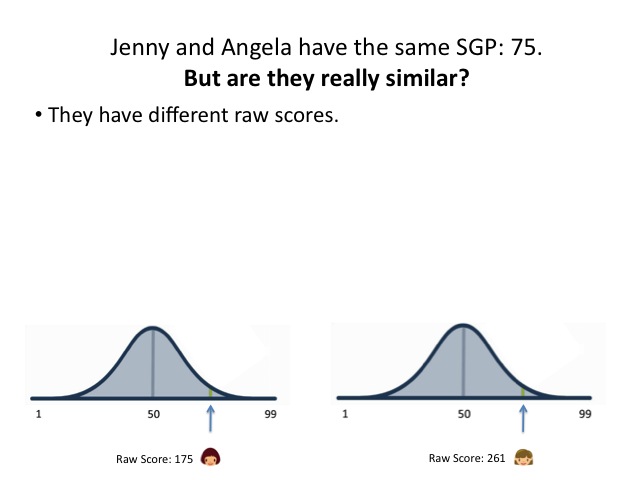
- The raw score, or achievement levels.
- The numeric growth.
- The "actual" growth in learning.
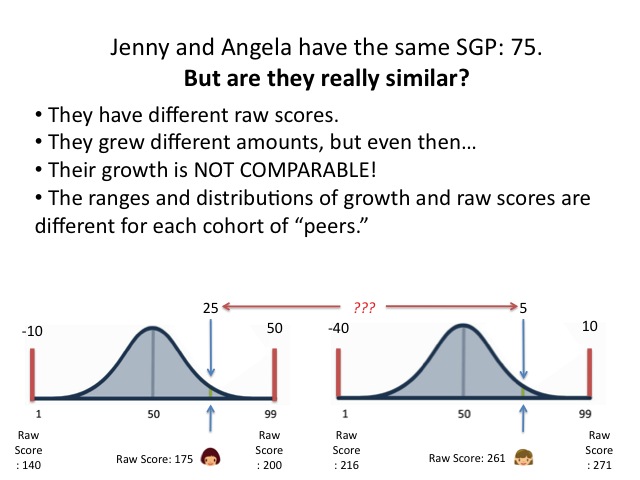
- The range of growth within the group of peers.
- The distribution of growth within the peers.
This blog post has been shared by permission from the author.
Readers wishing to comment on the content are encouraged to do so via the link to the original post.
Find the original post here:
The views expressed by the blogger are not necessarily those of NEPC.